1. ME-model Fundamentals¶
Models of metabolism and expression (ME-models) are unique in that they are capable of predicting the optimal macromolecular expression required to sustain a metabolic phenotype. In other words, they are capable of making novel predictions of the amount of individual protein, nucleotides, cofactors, etc. that the cell must synthesize in order to grow optimally. To enable these types of predictions, ME-models differ from metabolic models (M-models) in a few key ways:
- ME-models are multi-scale in nature so they require the addition of coupling constraints to couple cellular processes to each other.
- ME-models predict the biomass composition of a growing cell thus forgoing much of the M-model biomass composition function. For this reason, the function representing growth needs to be updated.
These two ME-model features are briefly described below. Their practical implementation is further outlined in Building a ME-model.
1.1. Coupling Constraints¶
Coupling constraints are required in an ME-model in order to couple a reaction flux to the synthesis of the macromolecule catalyzing the flux. The easiest example of this is for the coupling of metabolic enzymes to metabolic reactions. This has the form:
where \(\mu\) is the growth rate and \(k_{eff}\) is an approximation of the effective turnover rate for the metabolic process. The coupling of enzyme synthesis cost to metabolic flux scales with \(\mu\) to represent the dilution of macromolecules as they are passed on the daughter cells. More macromolecules are therefore diluted at faster growth rates. Enzyme turnover rates determine the efficiency of of an enzyme in vivo and are largly unknown for a majority of metabolic and expression-related enzymes. Optimizing the vector of \(k_{eff}s\) for the cellular processes modeled in the ME-model is an ongoing area of research.
Currently for the E. coli ME-model, the \(k_{eff}s\) are set with an average of 65 \(s^{-1}\) and scaled by their solvent accessible surface area (approximated as \(protein\_moleculare\_weight^{\frac{3}{4}}\)). A set ~125 metabolic \(k_{eff}s\) were found by Ebrahim et. al. 2016 to be particularly important in E. coli for computing an accurate metabolic/proteomic state using proteomics data. We suspect similar observations would be seen in other organisms.
For non metabolic macromolecules such as ribosome, mRNA, tRNA and RNA polymerase, the coupling constrains coefficients (‘\(k_{eff}s\)‘) are derived by essentially back-calculating the individual rates using a measured RNA-to-Protein ratio from Scott et. al. 2010 and measured mRNA, tRNA and rRNA fractions. The coupling constraints coefficients for these macromolecules are derived in detail in O’Brien et. al. 2013. Applying these constraints results in a final nonlinear optimization problem (NLP) shown below. COBRAme reformulates these coupling constraints to embed them directly into the reaction which they are used as follows:
The biomass_dilution constraint is discussed below.
1.1.1. Previous ME-model Coupling Constraint Implementation¶
The previous iterations of ME-models applied coupling constraints using three separate reactions. An example for a generic “enzymatic reaction” could be represented as follows:
Where \(\alpha\) is the coupling coefficient applied to “coupling”, a metabolite (constraint) which effectively determines the minimal rate that the third dilution coupling reaction (\(v2\)) must proceed. For previous ME-model implementations, this coupling constraint was given a “_constraint_sense” in COBRApy of ‘L’ (less than or equal to) meaning that for this toy example \(v0 = v1\) and \(v2 \geq \alpha \cdot v1\).
1.1.2. COBRAme Coupling Constraint Implementation¶
With COBRAme it is assumed that the optimal ME solution will never dilute more enzyme than is required by the coupling constraint thus constraining \(v2 = \alpha \cdot v1\) and allowing us to combine the implementation of the constraint with the reaction that uses the enzyme to give.
The coupling constraints and coefficients were derived as in O’Brien et. al. 2013. As stated above, however, these were implemented in the current study as equality constraints . Effectively, this means that each ME-model solution will give the computed optimal proteome allocation for the in silico conditions. Previous ME-model formulations have applied the constraints as inequalities thus allowing the simulation to overproduce macromolecule components. While overproduction is seen in vivo in cells, this phenomenon would not be selected as the optimal solution. Furthermore, using inequality constraints greatly expands the size of the possible solution space significantly increasing the time required to solve the optimization. Reformulating the model using equality constraints thus resulted in a reduced ME-matrix with the coupling constraints embedded directly into the reaction in which they are used.
1.2. Biomass Dilution Constraints¶
For metabolic models (M-models), the biomass objective function has been used to represent the amount of biomass production that is required for the cell to double at a specified rate. The metabolites represented in the biomass function are typically building blocks for major macromolecules (e.g. amino acids and nucleotides), cell wall components and cofactors. The coefficients of the biomass objective function are determined from empirical measurements from a cell growing at a measured rate. Since ME-models explicitly compute the predicted amount of RNA, protein, cofactors, etc. necessary for growth, this concept has to be modified for ME-models.
This is accomplished via the biomass_dilution variable (reaction), which contains a biomass constraint (pseudo metabolite) that represents the mass produced by the synthesis of each functional RNA or protein. This reaction essentially ensured that the ME-model can only produce biomass at the rate it is being diluted (via growth and division).
1.2.1. Implementation¶
For each transcription or translation reaction in an ME-model an amount of a biomass constraint (pseudo metabolite) is created with a stoichiometry equal to the molecular weight of the mRNA or protein being made (in kDA). The below figure shows an example of this where a translation reaction produces both the catalytic protein as well as the protein biomass constraint. The formed protein_biomass constraint is a participant in the overall ME-model Biomas_ Dilution reaction which restricts the total production of the major biomass components to equal the rate at which biomass is diluted (i.e. the cell’s growth rate, \(\mu\)).
Some biomass constituents do not have a mechanistic function in the ME-model (e.g. cell wall components, DNA and glycogen). These metabolites are included in the biomass_dilution reaction indentical to the M-model biomass reaction .
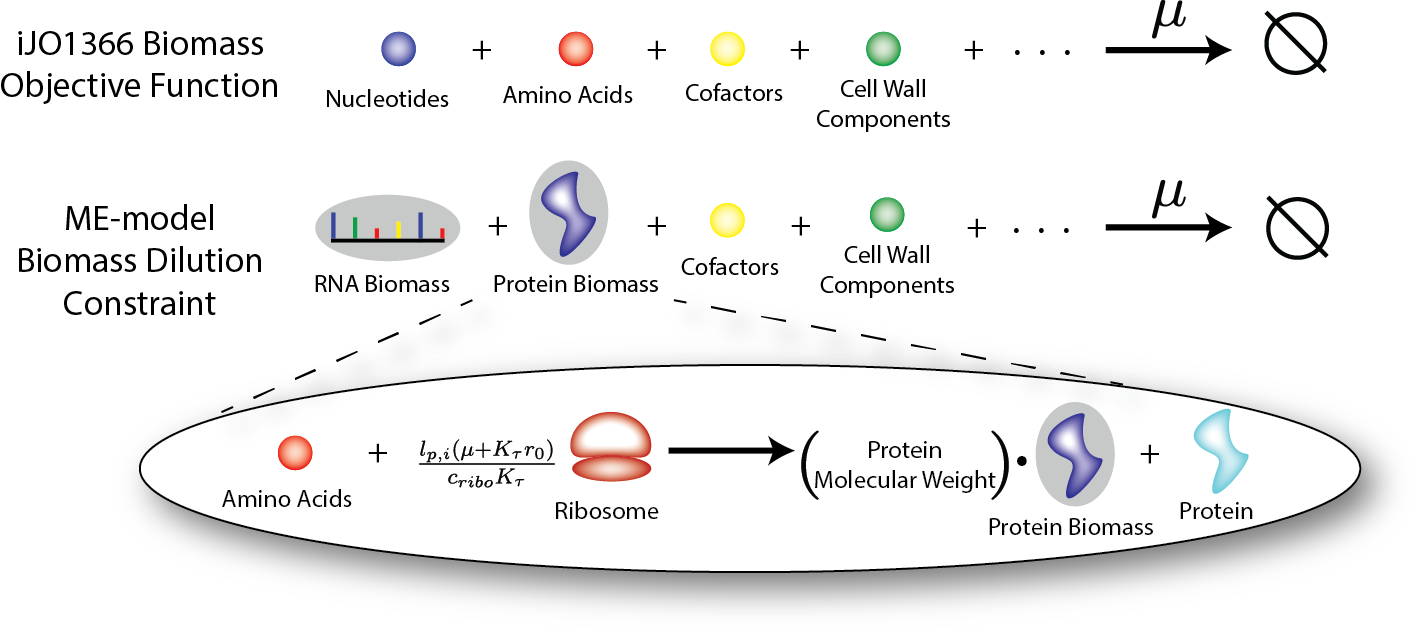
Biomass Dilution for iJO1366 and for a ME-model
1.2.2. Unit Check¶
The units for this contraint work out as follows:
The units of a given reaction in the ME-model are in molecules per hour.
The individual components of the biomass dilution constraints are in units of kDa.
Therefore, when the biomass dilution variable (reaction) carries flux it gives units of \(hr^{-1}\) representing the growth rateof the cell, \(\mu\)